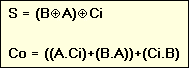Le nombre binaire Co S, Co étant le bit de poids le plus fort (MSB) et S le bit de poids le plus faible (LSB), est le résultat de l’addition des 3 nombres binaires A, B et Ci.
On remarquera que Co est la retenue de l’addition (Carry out).
 |
 |
 |
|
|||||||||
| Ce circuit permet d’additionner 2 nombres de 1 bit, A et B, et éventuellement 1 autre nombre de 1 bit, Ci (Carry in), pouvant représenter la retenue d’une addition antérieure. | |||||||||
| Le plus grand nombre décimal que l’on peut obtenir en additionnant 3 nombres binaires de 1 bit est 3 (1+1+1=3). | |||||||||
| Il faut donc 2 bits, Co et S, pour écrire en binaire le résultat de l’addition. En effet, en binaire 3 s’écrit 11. | |||||||||
|
Le nombre binaire Co S, Co étant le bit de poids le plus fort (MSB) et S le bit de poids le plus faible (LSB), est le résultat de l’addition des 3 nombres binaires A, B et Ci. On remarquera que Co est la retenue de l’addition (Carry out). |
|||||||||
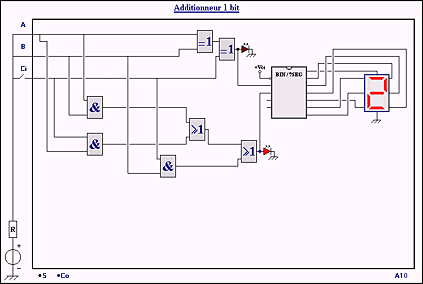
| Enfin, un décodeur BCD / 7 segments permet de visualiser le résultat de l’addition sur un afficheur à 7 segments. | |||||||||
|
|||||||||
| Dans l’exemple ci-dessus, les nombres binaires A, B et Ci sont respectivement égaux à 1, 1 et 0. Le résultat de l’addition de ces 3 nombres s’écrit 10 en binaire (2 en décimal). Le bit Co est donc égal à 1 (diode correspondante allumée) et le bit S est égal 0 (diode correspondante éteinte). | |||||||||
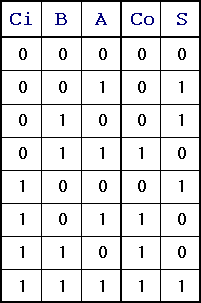
| Equations Logiques et Table de vérité : | |||||||||
|
|||||||||
|
|||||||||
|
|
|||||||||
|
|||||||||
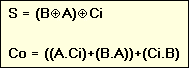